Radioactivity
Posted by Arms Control Center in BASIC SCIENCE, tags: half-life, Radioactive Decay, Radioactivity, Radioactivity Laws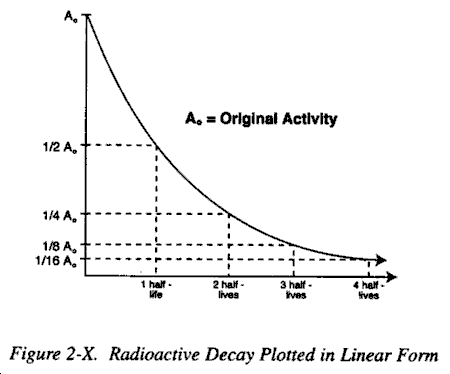 Radioactivity.
Radioactivity.
The nuclei of certain naturally occurring isotopes, and of others produced artificially, contain excess energy, i.e., they are unstable. To attain stability, nuclei with excess energy emit that energy in the form of nuclear, ionizing radiation and, in that process, frequently change into different elements. (See paragraph 215e.) (Ionizing radiation is defined as radiation capable of removing an electron from a target atom or molecule, forming an ion pair.) Isotopes, the nuclei of which emit ionizing radiations to achieve stability, are termed radioactive. Radioactive isotopes are referred to as radioisotopes or radionuclides.
a. Radioactive Decay. The process wherein radionuclides emit ionizing radiation is also termed radioactive decay. Each radioisotope has its own characteristic decay scheme. A decay scheme identifies the type or types ionizing radiation emitted; the range of energies of the radiation emitted; and the decaying radioisotope’s half-life.
b. Half-Life. Half-life is defined as the time required for half of the atoms of a given sample of radioisotope to decay. Half-life values range from fractions of a millionth of a second to billions of years. Theoretically, no matter how many half-lives have passed, some small number of nuclei would remain. However, since any given sample of radioactive material contains a finite number of atoms, it is possible for all of the atoms eventually to decay.
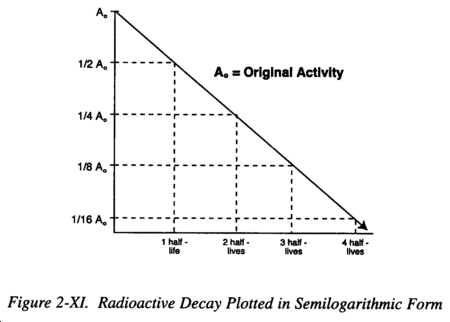
c. Data Plotting. Radioactive decay may be plotted in a linear form as shown in Figure 2-X or in a semilogarithmic form as in Figure 2-XI. The latter has the advantage of being a straight lineplot. The straight line form is used extensively in radiation physics, particularly when dealing with isotopes with short half-lives, since it allows direct determination by simple inspection of the activity at any given time with a precision adequate for most purposes.
214. Measurement of Radioactivity.
a. The international system of units is based on the meter, kilogram, and the second as units of length, mass, and time, and is known as Systems International (SI). The amount of radioactivity in a given sample of radioisotope is expressed by the new Systems International (SI) unit of the Becquerel (Bq). The old unit was the Curie (Ci). One Becquerel of a radioisotope is the exact quantity that produces one disintegration per second. The Curie is 3.7 x 1010Bq disintegrations per second. Thus 1 Bq = 2.7 x 10-11Ci and 1 Ci = 3.7 x 1010Bq. As the Becquerel is inconveniently small for many uses as was the Curie inconveniently large, prefixes such as micro (�) (10-6), milli (m) (10-3), kilo (k) (103), mega (M) (106), and giga (G) (109) are routinely used. Following nuclear detonations, the amounts of radioactive material produced are very large and the terms pets-becquerel (PBq) (1015Bq) and exabecquerel (EBq) (10l8Bq) may be used. The term megacurie (MCi) (106Ci) used to be used.
b. The amount of radioactive material available at any time can be calculated by using a specific mathematical formula:
from which the following can be derived
| since |
c. The terms in these formulae are as follows:
(1) At = activity remaining after a time interval, t.
(2) Ao = activity of sample at some original time.
(3) e = base of natural logarithms (2.718…).
(4)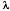 = decay constant of the particular isotope, derived from the half-life.
= decay constant of the particular isotope, derived from the half-life.
(5) t = elapsed time.
(6) T1/2 = half-life of the particular isotope.
d. This formula can be used to calculate the activity (A) of an isotope after a specific time interval (t) if the half-life (T1/2) and the original activity (Ao) are known.
(1) Example: If 3.7 x 1010Bq (= 1.0 Ci) of 6oCo (cobalt) is the original amount of radioactive material at time to, what will be the activity of the 60Co remaining 1 month later?
A1 month = activity remaining after 1 month (t)
A0= 3.7 x = 10 10Bq (original activity)
T1/2 = 5.27 years (half-life of 60Co is 5.27 years)
t = 1 month (time elapsed since the original time).
(2) Substituting in the formula gives the following:
(4) In other words, the activity of 60Co after 1 month is 0.99 of its original activity, a reduction of only 1%. This could not be determined with precision from a graphic plot of activity versus time.
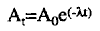
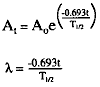
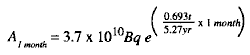
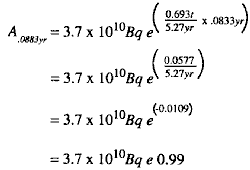

 Entries (RSS)
Entries (RSS)