 Atomic Mass Unit.
Atomic Mass Unit.
a. Common units of mass, such as grams, are much too large to conveniently describe the mass of an atomic nucleus or any of its constituent parts. To solve this problem a new unit was defined: the atomic mass unit (amu). The atomic mass unit is a relative unit defined arbitrarily by assigning a mass of 12 amu to the neutral atom carbon-12, the common isotope of carbon. One atomic mass unit equals 1.66 X 10-24 grams. Employing this value, the masses of the fundamental particles of an atom have been determined to be:
(1) Proton mass: 1.00727 amu.
(2) Neutron mass: 1.00867 amu.
(3) Electron mass: 0.00055 amu.
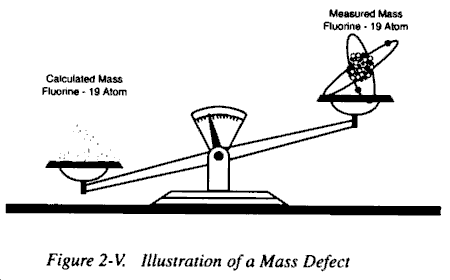
b. Logically, it should be possible, knowing the number of particles comprising a particular atom, to calculate the mass of that atom. However, experiments have shown that the total mass of an atom is less than the sum of the masses of the atom’s electrons, protons, and neutrons. For example, the measured mass of the isotope fluorine-19 atom is 18.99840 amu, while the sum of the masses calculated for the individual particles of that atom is 19.15708 amu. The difference of 0.15868 amu between the measured and calculated mass of the fluorine-19 atom is defined as the mass defect.
c. Careful experimentation and study have shown that while the mass defect is real, the law of conservation of mass has not been violated. When basic particles combine to form an atom, a certain amount of mass is lost through conversion into energy in accordance with Einstein’s equation E = mc2, where E is the energy, m is the mass, and c is the velocity of light in a vacuum. The converted energy is considered to be binding energy, i.e., energy necessary to hold the nucleus together.
source

 Entries (RSS)
Entries (RSS)
địa lý
Atomic Mass Unit |Arms Control Center » Arms Control Center
f
Atomic Mass Unit |Arms Control Center » Arms Control Center